3164 - 编程实现:小松鼠的聚会
在一片树林中,有 n个树洞,按顺序从 1到 n 编号,每个树洞里住着至少一只松鼠。
一条藤蔓连接两个树洞,共有 n-1条藤曼,使得任意两个树洞可以直接或间接到达。这些小松鼠经常举办聚会,当某个树洞中的小松鼠举办聚会时,它们也会邀请距离自家树洞不超过 k 条藤蔓范围的邻居们前来参加聚会。
请计算出每个树洞分别在举办聚会时,最多有多少只小松鼠参加聚会并按照树洞编号从 1到 n 依次输出结果。
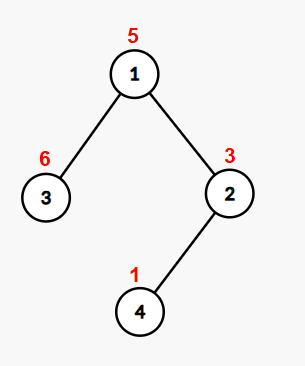
例如;n=4,表示有 4 个树洞, 1到 4号树洞中居住的小松鼠的数量分别为:5、3、6、1。
共有 3 条藤蔓,每条藤蔓连接两个树洞,分别为:1 和2、1 和3、2和4;
k = 2,表示当某个树洞中的小松鼠举办聚会时,它们会邀请距离自家树洞不超过2条藤葛范围的邻居们前来参加聚会。
根据上图得知:
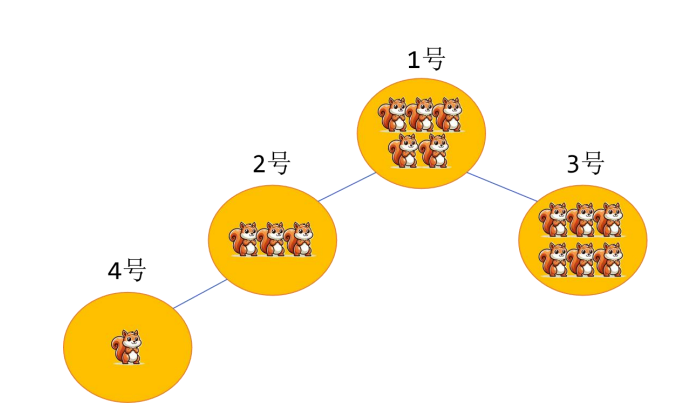 当 1 号树洞的小松鼠举办聚会时,1、2、3、4号树中的小松鼠可以参加,最多会有15(5 + 3 + 6+1)只小松鼠参加;
当 1 号树洞的小松鼠举办聚会时,1、2、3、4号树中的小松鼠可以参加,最多会有15(5 + 3 + 6+1)只小松鼠参加;
当 2 号树洞的小松鼠举办聚会时,1、2、3、4号树洞中的小松鼠可以参加,最多会有 15(5 +3 +6+1) 只小松鼠参加;
当3号树洞的小松鼠举办聚会时,1、2、3号树洞中的小松鼠可以参加,最多会有14(5 +3 +6)只小松鼠参加;
当4 号树洞的小松鼠举办聚会时,1、2、4 号树洞中的小松鼠可以参加,最多会有 9(5+3 + 1)只小松鼠参加;
故答案为15 15 14 9
第一行输入一个整数 n(1<=n<=100000),表示树洞的数量
接下来.n 行,每行输入一个整数 Ci( 1<=Ci<=1000)分别表示1到n号树洞中居住的小松鼠的数量,
接下来n- 1行,每行输入两个整数 ai,bi( 1<=ai, bi<=n)表示藤蔓连接两个树洞的编号,整数之间以一个空格隔开
最后一行输入一个整数 k(1<=k<=20),表示邀请邻居的距离限制。
共n行,每行输出一个整数,表示每个树洞中的小松鼠在举办聚会时,参加聚会的小松鼠的最大数量,按照树洞编号从 1 到n依次输出结果。
输入
4 5 3 6 1 1 2 1 3 2 4 2
输出
15 15 14 9
输入
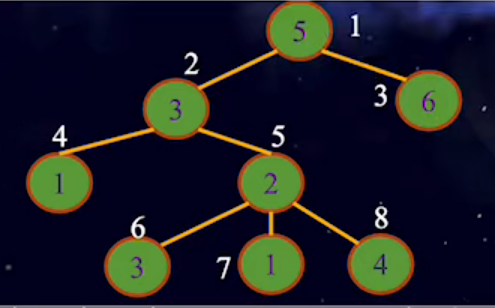
8 5 3 6 1 2 3 1 4 1 2 1 3 2 4 2 5 5 6 5 7 5 8 3
输出
25 25 17 25 25 19 19 19
下图为样例2对应的图
蓝桥杯